Simplification Of K-Map (Karnaugh Map)

The logic simplification examples that we have done so could have been performed with Boolean algebra about as quickly. Real world logic simplification problems call for larger Karnaugh maps so that we may do serious work. We will work some contrived examples in this section, leaving most of the real world applications for the Combinatorial Logic chapter. By contrived, we mean examples which illustrate techniques. This approach will develop the tools we need to transition to the more complex applications in the Combinatorial Logic chapter.

We show our previously developed Karnaugh map. We will use the form on the right.

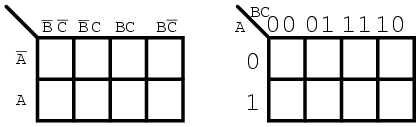
Note the sequence of numbers across the top of the map. It is not in binary sequence which would be 00, 01, 10, 11. It is 00, 01, 11 10, which is Gray code sequence. Gray code sequence only changes one binary bit as we go from one number to the next in the sequence, unlike binary. That means that adjacent cells will only vary by one bit, or Boolean variable. This is what we need to organize the outputs of a logic function so that we may view commonality. Moreover, the column and row headings must be in Gray code order, or the map will not work as a Karnaugh map. Cells sharing common Boolean variables would no longer be adjacent, nor show visual patterns. Adjacent cells vary by only one bit because a Gray code sequence varies by only one bit.

If we sketch our own Karnaugh maps, we need to generate Gray code for any size map that we may use. This is how we generate Gray code of any size.

*Important:

Notice that this edge numbering does not follow the normal binary counting sequence, but uses a Gray Code sequence where only one bit changes from one cell to the next. This is an important feature of Karnaugh maps; get the sequence wrong and the map will not work.

For more information about k-map watch this video-

credit goes to-http://www.allaboutcircuits.com and raj kumar for video